Some Necessary Conditions
Theorem 1: A necessary condition for convergence of the linear multistep method (8.1) is that the modulus of no root of the associated polynomial 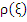 exceeds one, and that the roots of modulus one be simple. exceeds one, and that the roots of modulus one be simple.
The condition thus imposed on 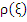 is called the condition of zero-stability. is called the condition of zero-stability.
Proof: If the method is convergent, it is convergent for the initial value problem 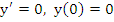 , whose exact solution is , whose exact solution is 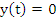 . For this problem (8.1) reduces to the difference equation with constant coefficients . For this problem (8.1) reduces to the difference equation with constant coefficients
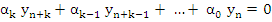 |
(8.11) |
If the method is convergent, then by (8.10), for any 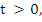
 |
(8.12) |
for all solutions 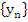 of (8.11) satisfying of (8.11) satisfying
 |
(8.13) |
where 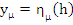 . Let . Let 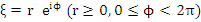 be a root of be a root of 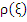 . Then, the numbers . Then, the numbers
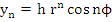 |
(8.14) |
|