Definition:
The linear multistep method defined by (8.1) is called Convergent , if the following statement is true for all functions 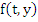 satisfying the existence and uniqueness conditions and all values of satisfying the existence and uniqueness conditions and all values of 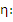 If If 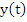 denotes the solution of the initial value problem denotes the solution of the initial value problem
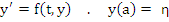
then
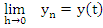 |
(8.9) |
holds for all 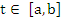 and all solutions and all solutions 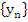 of the difference equation (8.1) having starting values of the difference equation (8.1) having starting values 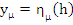 satisfying satisfying
 |
(8.10) |
It should be noted that this definition requires that condition (8.9) be satisfied not only for the sequence 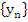 defined with the exact starting values- for these (8.10) is certainly satisfied- but also for all sequences whose starting values tend to the right value as defined with the exact starting values- for these (8.10) is certainly satisfied- but also for all sequences whose starting values tend to the right value as 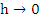 . This more stringent condition is imposed because in practice it is almost never possible to start a computation with mathematically exact values. . This more stringent condition is imposed because in practice it is almost never possible to start a computation with mathematically exact values. |