where the coefficients 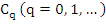 are constants which do not depend on the choice of the function are constants which do not depend on the choice of the function 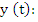
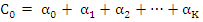
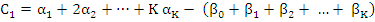
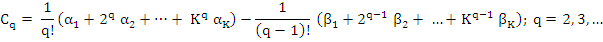
A given difference operator of the form (8.2) is said to be of order p if 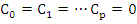 , but , but 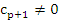 . As in the case of one-step methods, the order may be considered as a first crude measure of the accuracy of the method. . As in the case of one-step methods, the order may be considered as a first crude measure of the accuracy of the method.
From the practical point of view the difference equation (8.1) is completely equivalent to the equation
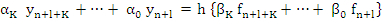 |
(8.3) |
where l is any fixed (positive or negative) integer. Proceeding as above,
we may associate with (8.3) the difference operator
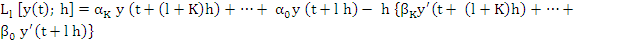 |
(8.4) |
and define its order as the order of the first non-vanishing term in its Taylor expansion in powers of h minus 1. It is an important fact that the order p as well as the constant Cp+1 do not depend on l . For, expanding (8.4) in powers of h is equivalent to expanding (8.2) in powers of 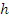 , where y(t) is replaced by , where y(t) is replaced by 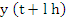 . We thus find, if L is of the order . We thus find, if L is of the order 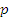 , , 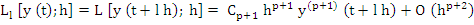
Since 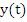 was assumed sufficiently differentiable, was assumed sufficiently differentiable,
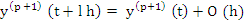
and thus
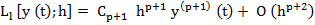
|