This proves the assertion, even without making use of the assumption that l was an integer.
As an example, consider the mid-point rule [Nystrom's method with 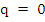 ], which in the standardized form (8.1) appears as follows: ], which in the standardized form (8.1) appears as follows:
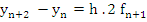
The corresponding operator (8.2) is given by
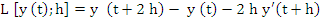
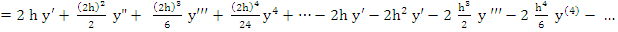
We readily find 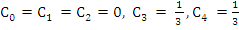 and thus and thus 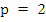 . .
Alternatively, by choosing 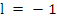 , we may consider the operator , we may consider the operator

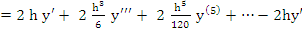
Again 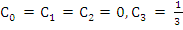 and hence and hence 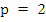 but now but now 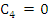 . This indicates that the constants . This indicates that the constants 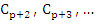 depend, in general, on depend, in general, on 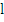 . From the point of view of practical computation, the second method of calculating p and . From the point of view of practical computation, the second method of calculating p and 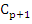 is clearly preferable, since in the Taylor's expansion only terms of odd order occur. is clearly preferable, since in the Taylor's expansion only terms of odd order occur.
The error constant of the method defined by (8.1) is

|