The associated difference operator; Order and error constant:
The condition of stability has the purpose of preventing a small initial error in the computation from growing at such a rate that convergence is jeopardized. It is clear, however, that stability alone does not guarantee convergence. A further condition must be added which ensures that the difference equation (8.1) is a good approximation to the differential equation 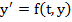 . .
When considering the problem of measuring the accuracy of a One-step method, we looked at the expression
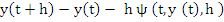 where where 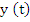 is a solution of the given differential equation. The smaller this quantity as a function of h, the higher was the accuracy of the method. Similarly, if (8.1) is to define a good method, we expect the discrepancy between the two sides of (8.1) to be small if h is small and if the values is a solution of the given differential equation. The smaller this quantity as a function of h, the higher was the accuracy of the method. Similarly, if (8.1) is to define a good method, we expect the discrepancy between the two sides of (8.1) to be small if h is small and if the values 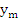 are replaced by are replaced by 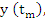 where where 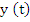 is an exact solution of the given differential equation. In order to measure this discrepancy, we associate with (8.1) the difference operator. is an exact solution of the given differential equation. In order to measure this discrepancy, we associate with (8.1) the difference operator.
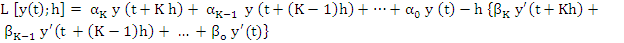 |
(8.2) |
This may be regarded as a linear operator that acts on any differentiable function 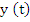 . For the time being, however, we shall apply the operator L only to functions which have continuous derivatives of sufficiently high order. We then may expand . For the time being, however, we shall apply the operator L only to functions which have continuous derivatives of sufficiently high order. We then may expand 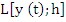 in powers of h, and the expansion can be pushed as far as we please. In view of the formulas in powers of h, and the expansion can be pushed as far as we please. In view of the formulas 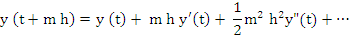
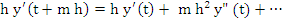
it turns out that
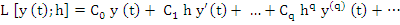
|