Introduction:
Most of the methods discussed earlier (particularly for 1st order equation) can be considered as a special case of the formula
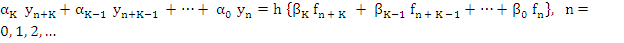 |
(8.1) |
where 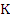 is a fixed integer, is a fixed integer,  and where and where 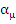 and and 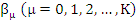
denote real constants which do not depend on 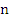 . We shall always assume that . We shall always assume that 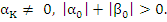 Equation (8.1) is said to define the General linear K-step method. The method is called linear because the values Equation (8.1) is said to define the General linear K-step method. The method is called linear because the values 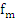 enter linearly in (8.1); it is not assumed that f is a linear function of y. enter linearly in (8.1); it is not assumed that f is a linear function of y.
One way in which we were able to derive the coefficients of Adams method was by requiring that they are exact for polynomials of degree 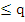 . There are . There are 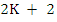 unknowns in (8.1). There is an arbitrary normalizing factor so we set unknowns in (8.1). There is an arbitrary normalizing factor so we set 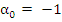 , leaving , leaving 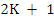 unknowns. unknowns.
Consequently, we expect to be able to choose the 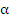 and and 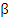 so that this method is exact for polynomials of degree upto so that this method is exact for polynomials of degree upto 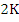 . This is possible. However, it has been observed that such methods are never useful for . This is possible. However, it has been observed that such methods are never useful for 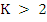 , and only marginally useful when , and only marginally useful when  . If we were only concerned with local truncation error and the problem had well-behaved derivatives, we would be tempted to use K-step methods of maximal order . If we were only concerned with local truncation error and the problem had well-behaved derivatives, we would be tempted to use K-step methods of maximal order 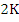 . But it is known that for . But it is known that for 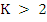 such methods cause the small truncation errors committed in one step to be unacceptably amplified in later steps due to instability. However, there are stable K-step methods of order such methods cause the small truncation errors committed in one step to be unacceptably amplified in later steps due to instability. However, there are stable K-step methods of order  (the Adams-Moulton method, for example) and order (the Adams-Moulton method, for example) and order  if K is even. if K is even. |