Let 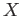 and
and 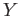 be topological spaces and
be topological spaces and
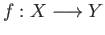 be a surjective continuous map such that
the given topology on
be a surjective continuous map such that
the given topology on 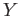 agrees with the quotient topology on
agrees with the quotient topology on 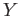 induced by
induced by 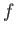 . Define an equivalence
relation
. Define an equivalence
relation 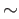 on
on 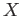 as follows:
as follows:
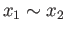
if and only if
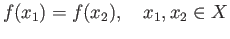
The identification space 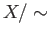 is homeomorphic to
is homeomorphic to 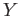 via the map
via the map
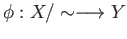 given by
given by
nisha
2012-03-20