It is easy to see that  is well-defined, bijective and satisfies
is well-defined, bijective and satisfies
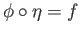 .
Since
.
Since  is continuous and
is continuous and 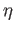 is a quotient map we see by the universal property that
is a quotient map we see by the universal property that  is continuous.
Since
is continuous.
Since  is a quotient map and
is a quotient map and 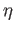 is continuous we may invoke the universal property again but this time
to
is continuous we may invoke the universal property again but this time
to
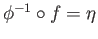 to conclude that
to conclude that 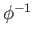 is continuous as well.
is continuous as well.
nisha
2012-03-20