Suppose that  is a topological space and
is a topological space and 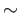 is an equivalence relation on
is an equivalence relation on
 . The set of all equivalence classes is denoted by
. The set of all equivalence classes is denoted by 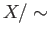 and
and
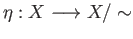 denotes
the projection map
denotes
the projection map
where
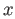 denotes the equivalence class of
denotes the equivalence class of 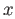 . The space
. The space 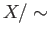 with the quotient topology
induced by
with the quotient topology
induced by 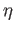 is called the identification space given by the equivalence relation. An important special
case deserves mention as it is of frequent occurrence. Suppose that
is called the identification space given by the equivalence relation. An important special
case deserves mention as it is of frequent occurrence. Suppose that  is a subset of a topological space then we
consider the equivalence relation for which all the points of
is a subset of a topological space then we
consider the equivalence relation for which all the points of  form one equivalence class and the equivalence
class of any
form one equivalence class and the equivalence
class of any
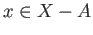 is a singleton. That is to say all the points of
is a singleton. That is to say all the points of  are identified together as one
point and no other identification is made. We shall refer to the resulting quotient space as
the space obtained from
are identified together as one
point and no other identification is made. We shall refer to the resulting quotient space as
the space obtained from  by collapsing
by collapsing  to a singleton.
to a singleton.
nisha
2012-03-20