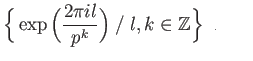- Prove that the map
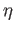 in the five lemma is surjective.
in the five lemma is surjective.
- Show that the map (38.2) is indeed an isomorphism. To prove that it is surjective use the decompositions
 int
int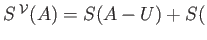 and
and
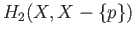 int
int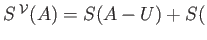 .
.
- Prove the Barrett-Whitehead lemma.
- Calculate the local homology groups
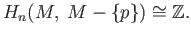 in the following cases:
in the following cases:
- (i)
- The space
 is the cylinder
is the cylinder
![$ S^1 \times [0, 1]$](img317.png) and
and  a point on its boundary.
a point on its boundary.
- (ii)
- The space
 is the Möbius band and
is the Möbius band and  is a point on its boundary.
is a point on its boundary.
Deduce that the cylinder and the Möbius band are not homeomorphic.
- A topological manifold is a Hausdorff space in which each point has a neighborhood homeomorphic
to an open ball in
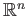 . Show that if
. Show that if  is a point on a topological manifold
is a point on a topological manifold 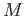 ,
,
in
Lecture - XXXIX (Test - V)
in
- Calculate the homology groups of the double torus.
- Show that any homeomorphism of
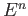 onto itself must preserve the boundary.
onto itself must preserve the boundary.
- Show that
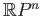 is not a retract of
is not a retract of
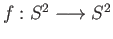 . Use the lifting criterion.
. Use the lifting criterion.
- Regard
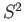 as the Riemann sphere and calculate the degree of the map
as the Riemann sphere and calculate the degree of the map
 given by
given by
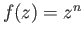 .
.
- Use the previous exercise to prove the fundamental theorem of algebra.
- Show that
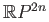 has the fixed point property. Does
has the fixed point property. Does
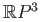 have the fixed point property?
have the fixed point property?
in
Lecture - XL Inductive limits
in
We have frequently encountered situations where a certain space  is canonically embedded in a larger space
is canonically embedded in a larger space  .
A familiar example the sequence of orthogonal groups and the canonical inclusions
.
A familiar example the sequence of orthogonal groups and the canonical inclusions
where, the inclusion map
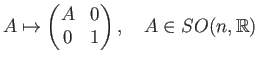 is given by
is given by
The inductive limit of a sequence such (40.1) is a space which contains each
individual member of the sequence, and is the smallest such space. The precise meaning of the adjective
smallest would be clear from the formal definition that we shall presently give.
Let us look at a situation in the category of abelian groups. For a fixed prime  let
let 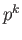 denote the cyclic
group of order
denote the cyclic
group of order 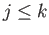 . Then for each
. Then for each 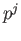 , the group
, the group 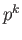 contains a (unique) cyclic group of order
contains a (unique) cyclic group of order 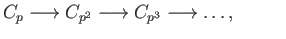 giving us a sequence of groups
giving us a sequence of groups
in which the arrows inclusion maps. All these groups may be regarded as subgroups of
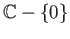 or as subgroups of
the smaller group
or as subgroups of
the smaller group 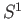 . However there is a smallest group containing a copy of each
the groups
. However there is a smallest group containing a copy of each
the groups 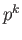 namely, the group
namely, the group
consisting of all 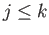 -th roots of unity (
-th roots of unity (
 ). This group (known as the Prüfer group)
would then be the inductive limit of the
family of cyclic groups
). This group (known as the Prüfer group)
would then be the inductive limit of the
family of cyclic groups 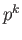 (
(
 ).
).
We now proceed to the formal definitions and prove the existence and uniqueness (upto isomorphism)
of the inductive limit of a family of groups. We recall the notion of a directed set.
Subsections
nisha
2012-03-20
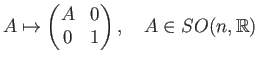 is given by
is given by
![]() let
let ![]() denote the cyclic
group of order
denote the cyclic
group of order ![]() . Then for each
. Then for each ![]() , the group
, the group ![]() contains a (unique) cyclic group of order
contains a (unique) cyclic group of order ![]() giving us a sequence of groups
giving us a sequence of groups