(i) Let 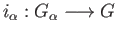 be the coproduct (direct sum)
of the abelian groups
be the coproduct (direct sum)
of the abelian groups
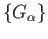 and we regard (for simplifying notations) the groups
and we regard (for simplifying notations) the groups
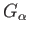 as being subgroups of
as being subgroups of 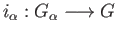 and
and
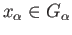 the inclusion maps.
Declare
the inclusion maps.
Declare
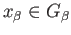 and
and
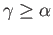 as being equivalent if there exists
as being equivalent if there exists
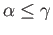 such that
such that
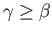 ,
,
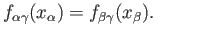 and
and
Lemma (40.1) states that this is a well defined equivalence relation.
We denote by 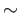 the equivalence relation just defined and define
the equivalence relation just defined and define  to be the subgroup generated by
to be the subgroup generated by
Finally let
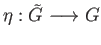 and
and
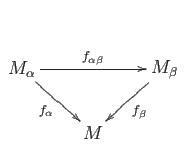
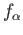 be the quotient map. We claim that
be the quotient map. We claim that  is
the inductive limit with respect to the maps
is
the inductive limit with respect to the maps
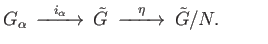 given by the composition
given by the composition
We now check the conditions (1) and (2) in definition (40.2). For
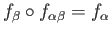 we derive from
we derive from
the useful piece of information
Hence
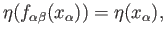 whereby we conclude
whereby we conclude
which in turn implies
 .
Turning to the universal property (2) assume given an abelian group
.
Turning to the universal property (2) assume given an abelian group  and a family of group homomorphisms
and a family of group homomorphisms
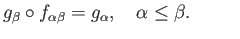 such that
such that
We first use the defining property of the coproduct to get a group homomorphism
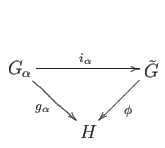 such that the following diagram commutes:
such that the following diagram commutes:
That is
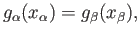 . From (40.4) and (40.7) we get
. From (40.4) and (40.7) we get
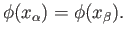 or in view of the fact that we have identified
or in view of the fact that we have identified
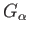 as a subgroup of
as a subgroup of
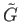 ,
,
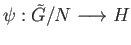 Hence there is a group homomorphism
Hence there is a group homomorphism
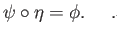 such that
such that
Upon applying this to an arbitrary
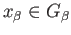 we get using (40.5) that
we get using (40.5) that
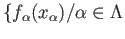 for every
for every
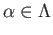 .
The homomorphism satisfying (40.8) is unique since the elements
.
The homomorphism satisfying (40.8) is unique since the elements
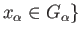 and
and 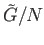 generate the group
generate the group
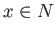 .
.
We now prove (ii) which we shall use in the next lecture. Since 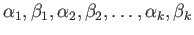 , there exists a finite set of
indices
, there exists a finite set of
indices
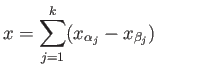 such that
such that
where
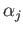 for each
for each 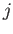 . Thus for each
. Thus for each 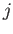 there is a
there is a 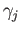 exceeding both
exceeding both
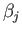 and
and 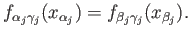 such that
such that
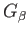 Since (40.9) spells out a relation in the direct sum of the groups
Since (40.9) spells out a relation in the direct sum of the groups 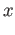 , it decomposes into a
bunch of equations namely
, it decomposes into a
bunch of equations namely
The index 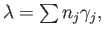 runs through a finite subset of
runs through a finite subset of
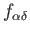 . Taking
. Taking 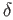 to
be sufficiently large and applying
to
be sufficiently large and applying
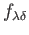 to the first and
to the first and
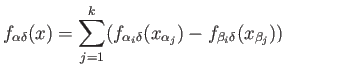 to the second of the above
displayed equations and adding we get
to the second of the above
displayed equations and adding we get
Using lemma (40.1) we see that if 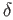 is sufficiently large each of the summands on the right hand side of
(40.10) is in
is sufficiently large each of the summands on the right hand side of
(40.10) is in 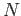 and so
and so
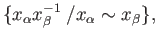 as asserted.
nisha
2012-03-20
as asserted.
nisha
2012-03-20
 .
Turning to the universal property (2) assume given an abelian group
.
Turning to the universal property (2) assume given an abelian group  such that the following diagram commutes:
such that the following diagram commutes:
![]() , there exists a finite set of
indices
, there exists a finite set of
indices
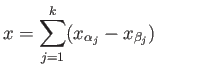 such that
such that
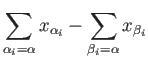
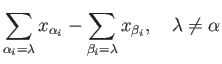
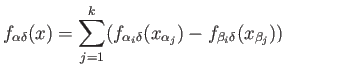 to the second of the above
displayed equations and adding we get
to the second of the above
displayed equations and adding we get