Given a directed system
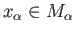 in one of the categories Gr, AbGr or Top and a family of morphisms
in one of the categories Gr, AbGr or Top and a family of morphisms
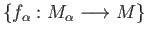 in the
same category satisfying the conditions in definition (40.1),
an inductive limit is an object
in the
same category satisfying the conditions in definition (40.1),
an inductive limit is an object 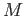 together with a family of
morphisms
together with a family of
morphisms
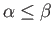 such that the following two conditions hold:
such that the following two conditions hold:
- (1)
- For every pair
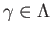 with
with
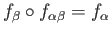 ,
,
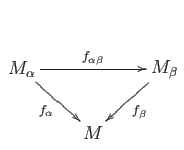 , summarized as a commutative diagram:
, summarized as a commutative diagram:
- (2)
- Universal property: Given an object
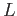 and a family of morphisms
and a family of morphisms
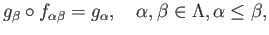 satisfying
satisfying
there exists a unique morphism
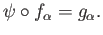 such that
such that
nisha
2012-03-20
 , summarized as a commutative diagram:
, summarized as a commutative diagram: