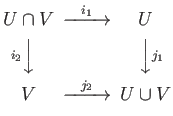(i) Let 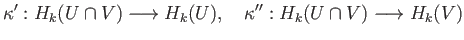 be an open covering of
be an open covering of  ,
,
be the maps induced by inclusions.
Further, let
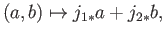 be the map:
be the map:
where 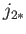 and
and 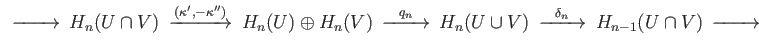 are induced by the respective inclusions
are induced by the respective inclusions
 and
and
 . Then, the
following long exact sequence known as the Mayer Vietoris sequence holds:
. Then, the
following long exact sequence known as the Mayer Vietoris sequence holds:
(ii) A cycle
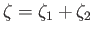 may be represented (modulo boundaries) as
may be represented (modulo boundaries) as
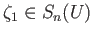 for some
for some
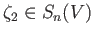 and
and
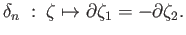 and the connecting homomorphism
and the connecting homomorphism
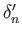 is given by
is given by
nisha
2012-03-20