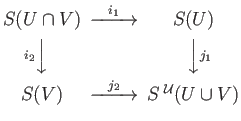In the diagrams below, the Left hand square depicts a push-out square of inclusions
which goes over to a push-out square of complexes on the right:
The reader may check that the latter may be recast as a short exact sequence of chain complexes namely
The corresponding long exact sequence in homology gives
The definition of
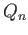 and exercise 6 enables us to
replace
and exercise 6 enables us to
replace 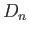 and
and 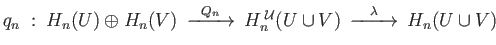 by the composites
by the composites
where 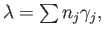 is the isomorphism given by theorem (34.6). The final result is the Mayer Vietoris sequence stated
in the theorem. The second part is clear from (29.18).
is the isomorphism given by theorem (34.6). The final result is the Mayer Vietoris sequence stated
in the theorem. The second part is clear from (29.18). 
nisha
2012-03-20