The first assertion follows from the comments preceding lemma (34.5). To show that
the inclusion maps induce an injective map on homologies, let
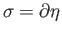 be a
singular chain such that
be a
singular chain such that
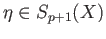 for some
for some
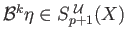 . Choose
. Choose
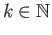 such that
such that
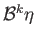 . We have to show that
. We have to show that
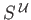 is a boundary in
is a boundary in
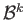 .
By exercise 5,
.
By exercise 5,
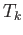 is chain homotopic to the identity via
a homotopy
is chain homotopic to the identity via
a homotopy 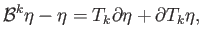 say. Applying
say. Applying 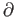 to
to
we see that
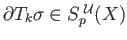 . By (ii) of lemma (34.5),
. By (ii) of lemma (34.5),
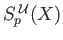 which means
which means
 is a boundary in
is a boundary in
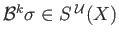 . To prove surjectivity, let
. To prove surjectivity, let  be a cycle in
be a cycle in 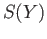 and
and
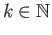 be such that
be such that
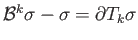 . From
. From
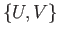 we conclude that
we conclude that  is homologous to the cycle
is homologous to the cycle
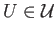 in
in
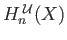 .
. 
nisha
2012-03-20