For each topological space  ,
there exists a unique chain map
,
there exists a unique chain map
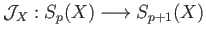 and a
chain homotopy
and a
chain homotopy
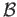 between
between 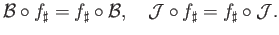 and the identity map,
which satisfies the following two conditions.
and the identity map,
which satisfies the following two conditions.
- (i)
- For a continuous map
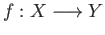 between topological spaces
between topological spaces  and
and  ,
,
- (ii)
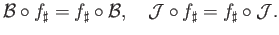 and
and 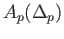 when restricted to the affine simplicies reduce to
when restricted to the affine simplicies reduce to 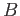 and
and 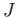 respectively.
respectively.
nisha
2012-03-20