Let 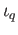 be the element of
be the element of
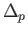 given by the identity map from
given by the identity map from 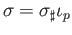 to itself.
Since an arbitrary
to itself.
Since an arbitrary
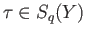 can be written as
can be written as
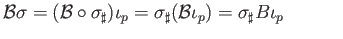 , condition (i) forces
, condition (i) forces
since
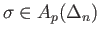 by (ii). Thus the conditions (i) and (ii) determine
by (ii). Thus the conditions (i) and (ii) determine 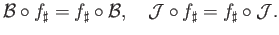 uniquely
on the generators of the free abelian group
uniquely
on the generators of the free abelian group 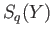 .
The same argument applies to
.
The same argument applies to 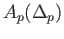 .
.
We use (34.10) and (34.5) to show
that 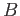 and
and 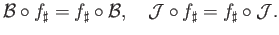 agree on any affine simplex
agree on any affine simplex
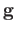 . Denoting by
. Denoting by 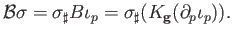 the barycenter of
the barycenter of 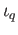 and by
and by 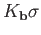 the barycenter of
the barycenter of  ,
,
Using exercise 2, this may be rewritten as
The verification for 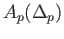 is similar. We now run through the proof that
is similar. We now run through the proof that
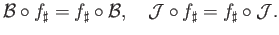 is a chain map, which is now automatic. For an
arbitrary
is a chain map, which is now automatic. For an
arbitrary
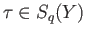 ,
,
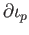 Since
Since
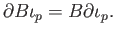 is an affine chain and
is an affine chain and 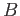 is a chain map on the
subcomplex of affine chains we get
is a chain map on the
subcomplex of affine chains we get
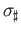 Applying
Applying
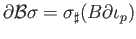 to this gives
to this gives
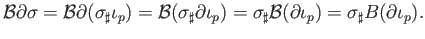 . Working from the other end
using the fact that
. Working from the other end
using the fact that
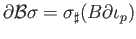 is a chain map and
is a chain map and 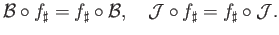 satisfies (i), we get
satisfies (i), we get
Finally we show that 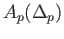 is a chain homotopy between
is a chain homotopy between 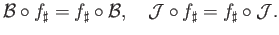 and the identity operator.
For
and the identity operator.
For
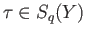 ,
,
We have used (i) and (ii) and the fact that
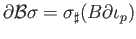 is a chain map. Subtracting and
using (34.9) we get the desired result.
is a chain map. Subtracting and
using (34.9) we get the desired result.  nisha
2012-03-20
nisha
2012-03-20
![]() and
and ![]() agree on any affine simplex
agree on any affine simplex
![]() . Denoting by
. Denoting by ![]() the barycenter of
the barycenter of ![]() and by
and by ![]() the barycenter of
the barycenter of ![]() ,
,