If 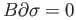 and
and  is a zero chain then
is a zero chain then
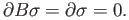 whereas
whereas
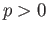 To handle the case
To handle the case  we assume inductively that for any
we assume inductively that for any 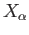 chain
chain  with
with
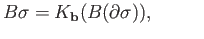 , the equation
, the equation
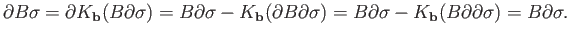 holds. To prove it for
holds. To prove it for  chains, let
chains, let  be an arbitrary affine
be an arbitrary affine
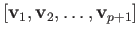 simplex. Equations (34.5) and (34.3) combine to give
simplex. Equations (34.5) and (34.3) combine to give
Note that induction hypothesis justifies
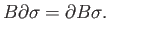 .
We have now shown that for every
.
We have now shown that for every  chain
chain  ,
,
We now construct a chain homotopy
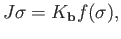 between
between 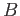 and the identity map.
Equation (34.3) suggests a formula of the type
and the identity map.
Equation (34.3) suggests a formula of the type
where 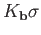 is the barycenter of
is the barycenter of  and
and
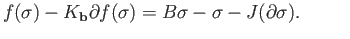 is to be determined. The condition that
is to be determined. The condition that 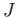 is a chain
homotopy between
is a chain
homotopy between 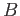 and the identity now forces
and the identity now forces
Clearly
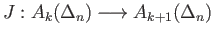 for a zero simplex
for a zero simplex  .
If we assume inductively that
.
If we assume inductively that
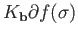 has already been defined for
has already been defined for
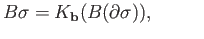 , the right hand side of (34.7) is then a known function. Let us refer to the term
, the right hand side of (34.7) is then a known function. Let us refer to the term
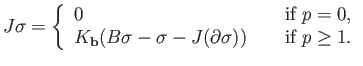 in equation (34.7) as junk. Exercise 3 invites the reader to check that
retaining the junk term is unnecessary. We set it equal to zero and define formally for a
in equation (34.7) as junk. Exercise 3 invites the reader to check that
retaining the junk term is unnecessary. We set it equal to zero and define formally for a  simplex
simplex  ,
,
Let us now verify that this formula does the job. The case 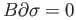 is trivial and let us assume
is trivial and let us assume
for any 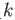 chain such that
chain such that
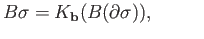 . Using the formula of
. Using the formula of 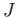 we see that
we see that
By induction hypothesis
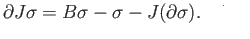 . Inserting this in (34.8) we get
the desired result
. Inserting this in (34.8) we get
the desired result
We shall now transfer the barycentric subdivision operator and the chain homotopy 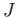 to a chain
map
to a chain
map
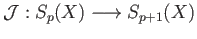 and a chain homotopy
and a chain homotopy
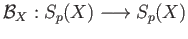 .
This will be unique subject to naturality.
nisha
2012-03-20
.
This will be unique subject to naturality.
nisha
2012-03-20
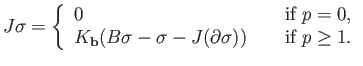 in equation (34.7) as junk. Exercise 3 invites the reader to check that
retaining the junk term is unnecessary. We set it equal to zero and define formally for a
in equation (34.7) as junk. Exercise 3 invites the reader to check that
retaining the junk term is unnecessary. We set it equal to zero and define formally for a