For each
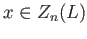 ,
,
We shall at some point as we go along, drop the primes and denote both sets of boundary maps by
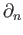 or even
or even 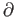 .
Observe that if
.
Observe that if
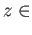 ker
ker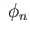 then
then
whereby we conclude that
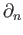 maps ker
maps ker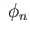 into ker
into ker
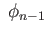 and we get a chain complex
and we get a chain complex
which we denote by ker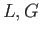 . Likewise we get the chain complex
. Likewise we get the chain complex
which we denote by Im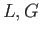 . It is clear from (29.13) that
. It is clear from (29.13) that
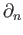 maps Im
maps Im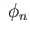 into Im
into Im
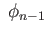 .
.
nisha
2012-03-20