(i) A differential chain complex is a sequence
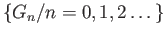 of abelian groups together with a sequence of
group homomorphism
of abelian groups together with a sequence of
group homomorphism
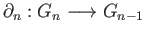 called the boundary operator satisfying the condition
called the boundary operator satisfying the condition
with the convention
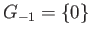 and
and
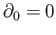 . We shall use the letter
. We shall use the letter  to denote this chain complex.
to denote this chain complex.
(ii) For a chain complex  , we define the subgroup
, we define the subgroup 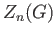 of
of  -cycles to be the kernel of
-cycles to be the kernel of
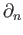 namely,
namely,
and the subgroup of  -boundaries as the image of
-boundaries as the image of
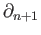 namely
namely
From (29.9) it is clear that
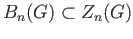 and also
and also
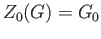 .
.
(iii) The quotient group
is called the  -th homology of the chain complex
-th homology of the chain complex  . If
. If
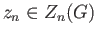 is a cycle the symbol
is a cycle the symbol
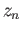 refers to the coset of
refers to the coset of 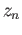 in the quotient group
in the quotient group 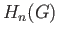 , called the homology class of
, called the homology class of 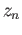 .
We shall simplify notations whenever feasible and write
.
We shall simplify notations whenever feasible and write 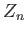 in place of
in place of 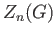 ,
, 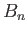 instead of
instead of 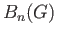 and
sometimes
and
sometimes
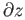 in place of the cumbersome
in place of the cumbersome
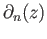 .
.
Given two chain complexes  and
and  one would like to study maps between them. These are the chain maps which
we now define.
one would like to study maps between them. These are the chain maps which
we now define.
nisha
2012-03-20
![]() , we define the subgroup
, we define the subgroup ![]() of
of ![]() -cycles to be the kernel of
-cycles to be the kernel of
![]() namely,
namely,
![]() and
and ![]() one would like to study maps between them. These are the chain maps which
we now define.
one would like to study maps between them. These are the chain maps which
we now define.