| |
Example 2.1
Consider a sequence of trials, each of which has two outcomes, but the outcomes are not independent of each other from trial to trail, as we would expect for the case when we toss a coin or do an experiment where the assumption of Bernoulli trail holds. Let us assume the transition probability matrix which dictates the relationship between the trials as: 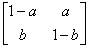 , also suppose that the initial condition as , also suppose that the initial condition as 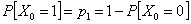 . What is of interest to us is to find (i) . What is of interest to us is to find (i) 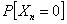 and (ii) and (ii) 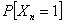 , so for which we should have: , so for which we should have:
(i) 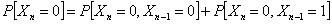 and and
(ii) 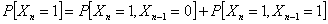
To find (i) and (ii) each of them can only come from either state 0 or 1, hence through method of induction we have: 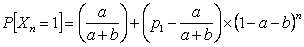 . .
Now 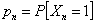 and and 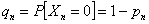 , hence we have , hence we have
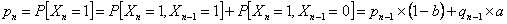
Furthermore  can be found in terms of can be found in terms of 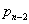 or or 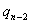 and so can and so can 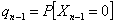 be found in terms of be found in terms of 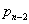 of of 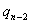 . If we extend this logic then one can find all the terms, and hence . If we extend this logic then one can find all the terms, and hence 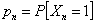 and and 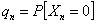 in terms of the initial conditions. in terms of the initial conditions.
|