| |
Example 2.2
Consider you have an experiment which consists of trials each of which has three (3) outcomes, and the trials are dependent and we have the transition probability matrix as 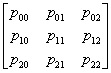 . Assume initial condition as . Assume initial condition as 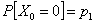 , , 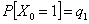 and and 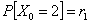 , with the additional conditional that , with the additional conditional that 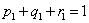 . Then find . Then find 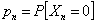 , , 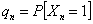 and and 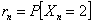 in terms of the transition probability values, in terms of the transition probability values, 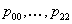 and and 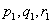 . .
Example 2.3
Let us further extend example 2.5, where you have an experiment which consists of 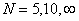 , trials. For the case , trials. For the case
(i) 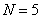 , each of the trial has 5 outcomes, and the trials are not independent but have the transition probability matrix such that , each of the trial has 5 outcomes, and the trials are not independent but have the transition probability matrix such that 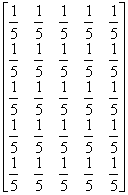 , ,
(ii) when 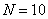 , each has 10 outcomes, and the trials are not independent but have the transition probability matrix such that , each has 10 outcomes, and the trials are not independent but have the transition probability matrix such that 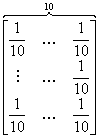 , ,
(iii) finally for the case 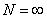 , each has , each has 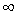 outcomes, and the trials are not independent but have the transition probability matrix given by Poisson distribution, outcomes, and the trials are not independent but have the transition probability matrix given by Poisson distribution, 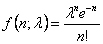 , with mean of 3 and remember that , with mean of 3 and remember that 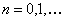 . .
For the three different sub-problem let us consider the initial conditions as (i) 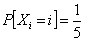 , , 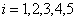 , (ii) , (ii) 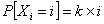 , , 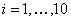 and (iii) Poisson distribution with mean of 3. With this set of information one can easily find (i) and (iii) Poisson distribution with mean of 3. With this set of information one can easily find (i) 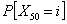 , for , for 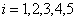 , , 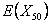 , , 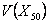 , (ii) , (ii) 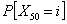 , for , for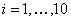 , , 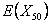 , , 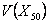 , (iii) , (iii) 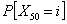 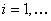 , for, , for, 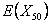 , , 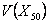 . . |