Chapman Kolmogorov Equation
First let us build the motivation for Chapman Kolmogorov equation. One is already aware that 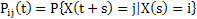 . Thus we are given the probability of the values such as . Thus we are given the probability of the values such as 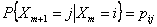 , which in general notation is denoted by , which in general notation is denoted by
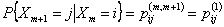 . .
Hence given 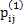 our main concern is to find our main concern is to find 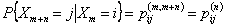 and we also want to comment intelligently whether this probability and we also want to comment intelligently whether this probability 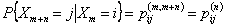 is dependent or independent on is dependent or independent on  . .
If we look carefully we will notice that in the equation 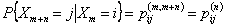 we do not have we do not have 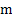 on the right hand side of the equation and such a process is called homogeneous Markov chain, otherwise a non-homogeneous Markov chain. on the right hand side of the equation and such a process is called homogeneous Markov chain, otherwise a non-homogeneous Markov chain.
Note
An example of a Markov chain may be when you play a gamble with a unbiased/biased coin or a dice and the transition probability values are generally independent of the state. Then you say that the Markov chain in homogeneous in nature. On the other hand if you have a drunken person who depending on his movement consumes an arbitrary amount of liquor as he/she moves to the right or left, then the transition probability values will be effected by the value of 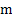 , and this type of process would be termed as non-homogenous Markov chain. , and this type of process would be termed as non-homogenous Markov chain.
Now from 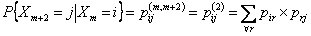 , we easily derive the fact that , we easily derive the fact that
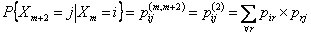
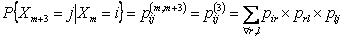 and so on and so on
Using the method of induction we can easily derive the general form as
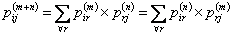 . .
The equation form is 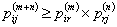 for any value of for any value of 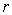 . Can you comment why this is be true? One should remember that for the case of homogeneous Markov chain we have: . Can you comment why this is be true? One should remember that for the case of homogeneous Markov chain we have: 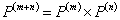
|