| |
Poisson process
Definition 1: A counting process denoted by  is said to be a Poisson process if it has the following three properties which are: is said to be a Poisson process if it has the following three properties which are:
 : Which means that the number of events when the process has just started is zero. : Which means that the number of events when the process has just started is zero.
- The process has independent increments.
- The number of events in the time interval
 , i.e., of length , i.e., of length  , where , where  can be of any length is Poisson distributed with mean can be of any length is Poisson distributed with mean  . Thus for all values of . Thus for all values of  and and  we have we have  , where , where  is the rate of the process. is the rate of the process.
Definition 2 : A counting process denoted by  is said to be a Poisson process with rate is said to be a Poisson process with rate  if it has the following four properties which are: if it has the following four properties which are:
 : This means the number of occurrences at time : This means the number of occurrences at time  , i.e., when the process has just started is zero. , i.e., when the process has just started is zero.
- The process has stationary (time homogeneity) and independent increments.
 : Which means that the probability of the number of events in the time interval : Which means that the probability of the number of events in the time interval  being exactly equal to 1 is equal to the product of the rate of the process and the time interval plus some incremental function of time interval, i.e., being exactly equal to 1 is equal to the product of the rate of the process and the time interval plus some incremental function of time interval, i.e., . .
 : The fourth property denotes that in case we are interested to find the probability that the number of events in the time interval : The fourth property denotes that in case we are interested to find the probability that the number of events in the time interval  is equal to 2 or more, then that probability becomes zero as the time interval shrinks or is made smaller and smaller. For the benefit of the reader we like to mention that a function is equal to 2 or more, then that probability becomes zero as the time interval shrinks or is made smaller and smaller. For the benefit of the reader we like to mention that a function  is said to be is said to be  if we have if we have 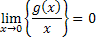
|