| |
Note
Definition # 1 and definition # 2 hold true in the iff sense which implies that definition # 1 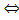 definition # 2. definition # 2.
Thus a Poisson process gives us the basic model for the arrival of some information based on which further studies may be done. Suppose we have a function that counts the number of times a specific event occurs, e.g., the number of gamma rays being emitted by a radioactive isotope in the time interval of 5 minutes, or the number of phone calls taking place within a time frame of say 1 hour, or the number of customers arriving at the bank teller counter within 5 hours, etc.
Using the same nomenclature used previously,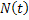 , would mean the number of events which occur in the time interval , would mean the number of events which occur in the time interval 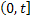 . One should understand and it is also quite obvious that this function, . One should understand and it is also quite obvious that this function,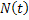 , is a non-decreasing step function, as shown in Figure 2.3. , is a non-decreasing step function, as shown in Figure 2.3.
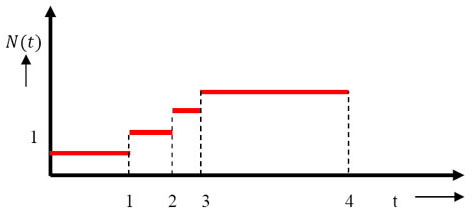 |
Figure 2.3: A hypothetical example of counting process which is also stationary process with respect to mean |
If 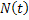 has a probability mass function, then it is necessary continuous. However continuous r.v. need not posses density function, and for that recall examples of a continuous and a discrete distribution function which are respectively of the forms has a probability mass function, then it is necessary continuous. However continuous r.v. need not posses density function, and for that recall examples of a continuous and a discrete distribution function which are respectively of the forms 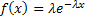 , ,  and and 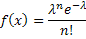 , , 
|