There are other two important properties for counting process worth mentioning and they are:
Independent increments: Which means that the numbers of events occurring between disjoint time intervals are independent. One can refer to Figure 2.1 which shows two disjoint time intervals and , such that numbers of events occurring in these two disjoint intervals which are respectively and are assumed to be independent.
Figure 2.1: Illustration of counting process and the concept of independent increments
Stationary increments : When a counting process is said to have stationary increments, then it means that the number of events that occur only depends on the length of the respective time interval and not on the time interval's end points.It also means that the number of events in the interval has the same distribution as the number of events in the interval . Thus if we refer to Figure 2.2 we see that the number of events shown in the green time interval and that of shown in the red time interval would have the same distribution. Furthermore one can comment that the number of events occurring between , where is positive depends on only and not on .
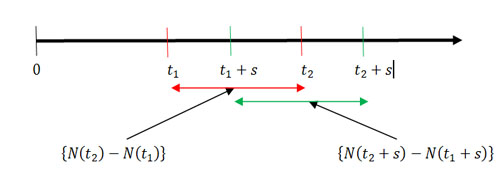
Figure 2.2: Illustration of counting process and the concept of stationary increments
Two important examples of counting process which we will consider in this course are (i) Poisson Process and (ii) Renewal process.
In this module/chapter we discuss in details the concepts of Poisson process and few interesting examples of Poisson process and the relevance of Kolmorogov equation and its use.
and 
, such that numbers of events occurring in these two disjoint intervals which are respectively 
and 
are assumed to be 
has the same distribution as the number of events in the interval 
. Thus if we refer to Figure 2.2 we see that the number of events 
shown in the green time interval and that of 
shown in the red time interval would have the same distribution. Furthermore one can comment that the number of events occurring between 
, where 
is positive depends on 
.
