| |
Definition of a Counting process
A stochastic process is said to be a counting process if represents the total number of events that have occurred up to time . One should remember that for many practical examples like how many times will the number 1 occur when one rolls a dice 15 number of times, or the numbers of red coloured cars passing through a certain road crossing/junction when one is standing at the junction for the past 1 hours, etc., can be cited as simple examples to illustrate the concept of a counting process.
In general a counting process should satisfy few properties which are as follows:
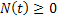 : Which is logical and implies that the number of occurrences of the event which we are interested to count should definitely be positive. : Which is logical and implies that the number of occurrences of the event which we are interested to count should definitely be positive.
 is an integer: This means that the number is always an integer and for the experiment when a person tosses a coin, then intuitively one can definitely comment that the number of heads one can get within a stipulated time can never be a fraction or decimal, but will always be an integer. is an integer: This means that the number is always an integer and for the experiment when a person tosses a coin, then intuitively one can definitely comment that the number of heads one can get within a stipulated time can never be a fraction or decimal, but will always be an integer.
- If
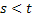 , then , then 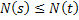 : Implies that it may be possible that the number of occurrences of the stochastic process within the stipulated time interval of : Implies that it may be possible that the number of occurrences of the stochastic process within the stipulated time interval of 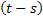 may be zero for which the number of arrivals in may be zero for which the number of arrivals in  , and , and 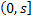 will always be the same, else the number of occurrences in the time interval will always be the same, else the number of occurrences in the time interval  will be greater than that in will be greater than that in 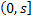 . .
- For
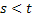 , , 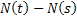 equals the number of events that have occurred in the time interval between equals the number of events that have occurred in the time interval between  and and  , i.e., , i.e.,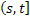 and this is a follow up of # 3. and this is a follow up of # 3.
|