| |
The flow chart of SORA is given in Figure 12.10, where in each cycle, the deterministic optimization is performed first, followed by reliability checking of gj(xMPP, d, pMPP) ≥ 0. If all of the probability constraints simultaneously fail to fulfill the reliability requirements, then the MPP information obtained in the current cycle will be used to formulate the deterministic optimization in the next cycle. This procedure is repeated until convergence is achieved. The number of function evaluations would be reduced, as the reliability assessment is now equal to the number of optimization cycles. To explain the strategy of separating deterministic optimization and reliability assessment while ensuring that both the segments work together to bring the design solution quickly to a feasible and optimal point, we consider Figure 12.9. As shown, Figure 12.9, if at the result of the deterministic optimization, the reliability constraint is not feasible, then its boundary, gj(xMPP, d, pMPP) = 0, in the optimization model is shifted towards the feasible region by a small distance, s = (s1,…, sJ), where 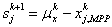 , based on the MPP recently found, so that this shift is performed in a manner that the MPP is moved onto the deterministic boundary, and the constraint in the deterministic optimization model are reformulated as , based on the MPP recently found, so that this shift is performed in a manner that the MPP is moved onto the deterministic boundary, and the constraint in the deterministic optimization model are reformulated as 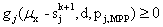 , , 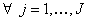 . The procedure is repeated until the objective converges and the reliability requirement is achieved when the shifting distances, . The procedure is repeated until the objective converges and the reliability requirement is achieved when the shifting distances, 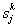 , , 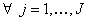 become zero. In order to improve the efficiency of SORA method, one may consider the starting point of inverse MPP search in any iteration as the MPP point obtained in previous iterations, and moreover similar starting point concept can be applied to the optimization cycle, where the optimal point of previous cycle is taken as the starting point. become zero. In order to improve the efficiency of SORA method, one may consider the starting point of inverse MPP search in any iteration as the MPP point obtained in previous iterations, and moreover similar starting point concept can be applied to the optimization cycle, where the optimal point of previous cycle is taken as the starting point.
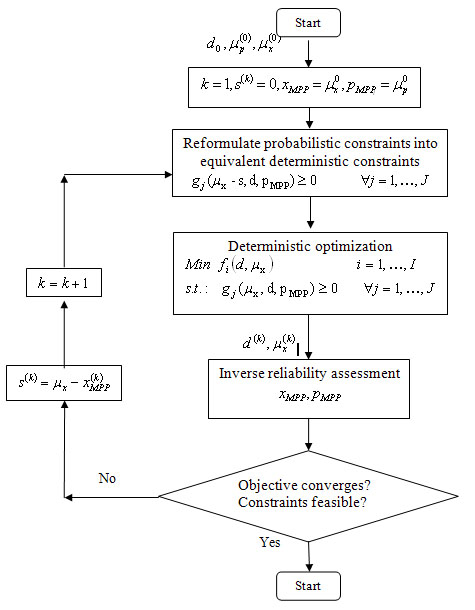
Figure 12.10: Flow Chart for SORA
So the stopping criteria for SORA method are based on the following two criteria, which are, (i) difference in the objective function between two consecutive cycles is less than a small e value, specified by the designer and (ii) all reliability requirements are satisfied. From the procedure of the SORA method we see that the reliability loop is completely decoupled from the optimization loop and in the optimization formulation, equivalent deterministic form of constraints, corresponding to the specified reliabilities, are used. As a result the computation requirements are reduced as compared to other methods.
|