Use of MCMC
We already know that when an item is put to use it will definitely fail after some time, and then it will be replaced by a new item of the same type and the time concept for finding the failure rate for the item will start again. The question we need to answer in such cases is what happens then when we need to find the best estimate of the time to failure and also the parameter values of the distribution based on which the items function. In case if we have bulbs, each of which have a time to failure given by the exponential distribution, then our main concern is to calculate the parameter,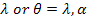 of that distribution and also of that distribution and also 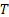 which would be the time to failure. This time to failure denotes when the first item (say A in Figure 12.11) fails such that the whole component fails. It may also be the case when we need to find the failure times for two items say E and F (Figure 12.11) such that the system stops functioning. which would be the time to failure. This time to failure denotes when the first item (say A in Figure 12.11) fails such that the whole component fails. It may also be the case when we need to find the failure times for two items say E and F (Figure 12.11) such that the system stops functioning.
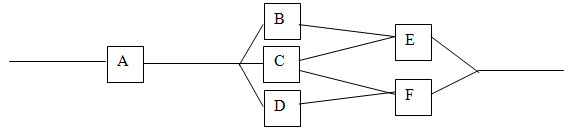
Figure 12.11: General set up for a system with series and parallel components
Based on this concept we have the competing-risk model which refers to a situation where a system (or organism) is exposed to two or more causes of failure (or death) but its eventual failure (or death) can be attributed to exactly one of the causes of failure. The basic information available in the competing-risks situation is the time to failure (T) of the system, and the corresponding cause of failure (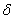 ). ).
|