| |
Sequential Optimization and Reliability Assessment (SORA)
Sequential Optimization and Reliability Assessment (SORA) works in a way in which a series of cycles of optimization task and reliability assessment are employed and in each such cycle, the optimization and reliability assessments are decoupled from one another i.e., no reliability assessment is required within optimization and the reliability assessment is conducted only after optimization process is complete. The key concept of the method is to shift the boundaries of the violated deterministic constraints to the feasible direction based on the information gained in the previous cycle such that both the optimization and reliability loops are repeated until convergence is achieved. Thus the three important steps for SORA are, (i) use 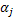 -percentile formulation to evaluate the design feasibility only at the desired reliability level -percentile formulation to evaluate the design feasibility only at the desired reliability level 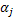 , (ii) employ equivalent deterministic optimization (first loop) to reduce the number of reliability assessments and (iii) use efficient MPP search algorithm for the reliability assessments loop. Note should made of the fact that the use of , (ii) employ equivalent deterministic optimization (first loop) to reduce the number of reliability assessments and (iii) use efficient MPP search algorithm for the reliability assessments loop. Note should made of the fact that the use of 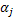 -percentile formulation instead of the original reliability assessment is based on the fact that, closer the reliability is to 1.0, more is the computational effort needed. Thus for using MPP based methods, higher reliability would mean higher search regions in the standard normal space to locate the MPP and it is more likely that more functional evaluations are required. Our concern for a probabilistic constraint is not to find the actual reliability of the limit state function, but to determine whether it is probabilistically feasible, as some probabilistic constraint(s) may never be active whose reliability is close to one, and if these constraint(s) is/are least critical, then the evaluation of this/these reliability/reliabilities may dominate the computational effort. Thus use of -percentile formulation instead of the original reliability assessment is based on the fact that, closer the reliability is to 1.0, more is the computational effort needed. Thus for using MPP based methods, higher reliability would mean higher search regions in the standard normal space to locate the MPP and it is more likely that more functional evaluations are required. Our concern for a probabilistic constraint is not to find the actual reliability of the limit state function, but to determine whether it is probabilistically feasible, as some probabilistic constraint(s) may never be active whose reliability is close to one, and if these constraint(s) is/are least critical, then the evaluation of this/these reliability/reliabilities may dominate the computational effort. Thus use of 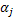 -percentile is performed to improve the efficiency of the overall process. Thus based on the relevant equations obtained after the MPP search is performed, the model given by (12.2) can be rewritten as shown in (12.6):Sequential Optimization and Reliability Assessment (SORA) -percentile is performed to improve the efficiency of the overall process. Thus based on the relevant equations obtained after the MPP search is performed, the model given by (12.2) can be rewritten as shown in (12.6):Sequential Optimization and Reliability Assessment (SORA)
Sequential Optimization and Reliability Assessment (SORA) works in a way in which a series of cycles of optimization task and reliability assessment are employed and in each such cycle, the optimization and reliability assessments are decoupled from one another i.e., no reliability assessment is required within optimization and the reliability assessment is conducted only after optimization process is complete. The key concept of the method is to shift the boundaries of the violated deterministic constraints to the feasible direction based on the information gained in the previous cycle such that both the optimization and reliability loops are repeated until convergence is achieved. Thus the three important steps for SORA are, (i) use 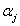 -percentile formulation to evaluate the design feasibility only at the desired reliability level -percentile formulation to evaluate the design feasibility only at the desired reliability level 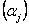 , (ii) employ equivalent deterministic optimization (first loop) to reduce the number of reliability assessments and (iii) use efficient MPP search algorithm for the reliability assessments loop. Note should made of the fact that the use of , (ii) employ equivalent deterministic optimization (first loop) to reduce the number of reliability assessments and (iii) use efficient MPP search algorithm for the reliability assessments loop. Note should made of the fact that the use of 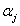 -percentile formulation instead of the original reliability assessment is based on the fact that, closer the reliability is to 1.0, more is the computational effort needed. Thus for using MPP based methods, higher reliability would mean higher search regions in the standard normal space to locate the MPP and it is more likely that more functional evaluations are required. Our concern for a probabilistic constraint is not to find the actual reliability of the limit state function, but to determine whether it is probabilistically feasible, as some probabilistic constraint(s) may never be active whose reliability is close to one, and if these constraint(s) is/are least critical, then the evaluation of this/these reliability/reliabilities may dominate the computational effort. Thus use of -percentile formulation instead of the original reliability assessment is based on the fact that, closer the reliability is to 1.0, more is the computational effort needed. Thus for using MPP based methods, higher reliability would mean higher search regions in the standard normal space to locate the MPP and it is more likely that more functional evaluations are required. Our concern for a probabilistic constraint is not to find the actual reliability of the limit state function, but to determine whether it is probabilistically feasible, as some probabilistic constraint(s) may never be active whose reliability is close to one, and if these constraint(s) is/are least critical, then the evaluation of this/these reliability/reliabilities may dominate the computational effort. Thus use of 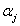 -percentile is performed to improve the efficiency of the overall process. Thus based on the relevant equations obtained after the MPP search is performed, the model given by (12.2) can be rewritten as shown in (12.6) : -percentile is performed to improve the efficiency of the overall process. Thus based on the relevant equations obtained after the MPP search is performed, the model given by (12.2) can be rewritten as shown in (12.6) :
SORA has been repeated twice. The second one is error free

|
(12.6) |
where 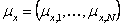 , , 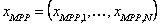 , , 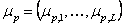 , and , and 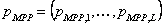 are the corresponding mean value vectors and the MPP vectors for the decision and parameter variables respectively. Thus, (12.6) establishes the relation between a probabilistic optimization and a deterministic optimization since the original constraint functions are the corresponding mean value vectors and the MPP vectors for the decision and parameter variables respectively. Thus, (12.6) establishes the relation between a probabilistic optimization and a deterministic optimization since the original constraint functions 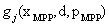 are used to evaluate the design feasibility using the inverse MPPs corresponding to desired reliability are used to evaluate the design feasibility using the inverse MPPs corresponding to desired reliability 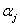 . One can refer to Figure 12.9 to understand how a probabilistic constraint is converted to equivalent deterministic constraint. . One can refer to Figure 12.9 to understand how a probabilistic constraint is converted to equivalent deterministic constraint.
|