| |
In PMA we calculate the MPP by formulating a minimization problem of the form: Minimize gj(ux, d, up), s.t. and this MPP is identified as the percentile performance level, calculated by and this MPP is identified as the percentile performance level, calculated by 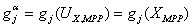 , i.e., the gj function evaluated at MPP. There are several methods to solve the MPP problem using PMA method, and that includes optimization techniques, traditional MPP search algorithm based on steepest ascent direction, the diagonal direction method and gradient based method, etc. On the other hand using RIA the MPP is calculated by finding a point which is on the constraint curve in the U-space and is nearest to the origin. The problem formulation corresponding to RIA approach is as follows: Minimize , i.e., the gj function evaluated at MPP. There are several methods to solve the MPP problem using PMA method, and that includes optimization techniques, traditional MPP search algorithm based on steepest ascent direction, the diagonal direction method and gradient based method, etc. On the other hand using RIA the MPP is calculated by finding a point which is on the constraint curve in the U-space and is nearest to the origin. The problem formulation corresponding to RIA approach is as follows: Minimize 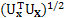 s.t. gj(ux, d, up) = 0. Here we ignore the desired reliability index βj and the minimum U vector on the constraint boundary is found. Afterwards this point thus found is compared with βj to get the optimal point. s.t. gj(ux, d, up) = 0. Here we ignore the desired reliability index βj and the minimum U vector on the constraint boundary is found. Afterwards this point thus found is compared with βj to get the optimal point.
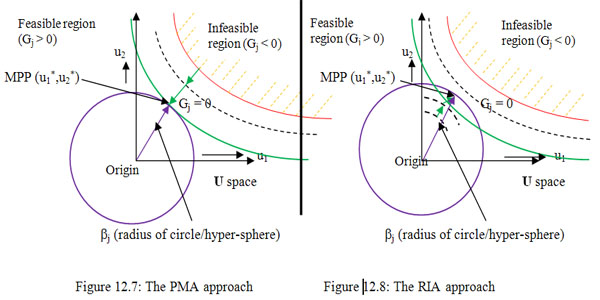
Figure 12.7 and Figure 12.8, give a pictorial illustration of both PMA and RIA methods, where the interesting fact to note is how the minimization is achieved. In PMA the constraint boundary (or one side of the hyper plane in n dimension space) at each iteration moves, which is shown by the red lines, while in RIA it is the boundary of the circle (or hyper sphere) which moves, that is again shown by the red lines. Hence reliability optimization problem involves two steps, which are (i) the requisite optimization technique to solve the problem and (ii) the reliability assessment method which is required to incorporate the uncertainty in the variables. In recent times the Sequential Optimization Reliability Assessment (SORA), a form of decoupled solution method has gained importance for reliability based optimization. |