Case 1: (Generalized Exponential Distribution (GED)) Bayesian case
In our model we utilize certain priors to obtain the Bayesian estimates for the GE distribution in the competing risks setup for complete data. Suppose we have a two component system connected in series. The failure distribution for component 1 and component 2 are given by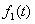 and and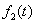 respectively.We assume that the scale parameter ( respectively.We assume that the scale parameter (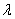 ) for both the components are same and the shape parameters are ) for both the components are same and the shape parameters are 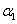 and and 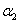 for component 1 and component 2 respectively.Let us consider n such systems which are identical to each other. for component 1 and component 2 respectively.Let us consider n such systems which are identical to each other.
As usual we assume that 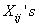 are distributed according to GE distribution for i=1,2,…n. are distributed according to GE distribution for i=1,2,…n.
We already know that 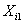 and and 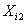 are the time to failure for the ith system due to component 1 and component 2 respectively and are the time to failure for the ith system due to component 1 and component 2 respectively and 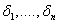 denote the cause of failure for the ith system where denote the cause of failure for the ith system where 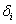 =1, 2. Then, the time to failure for the ith system will be the minimum of the two,i.e. =1, 2. Then, the time to failure for the ith system will be the minimum of the two,i.e. 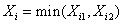
The likelihood function for the observed data 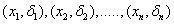
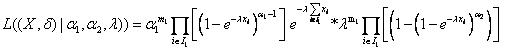 *
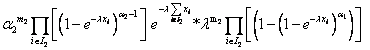 |
Since both 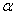 and and 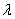 are non negative, we assume priors for are non negative, we assume priors for 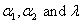 to be gamma priors.In many situations, the information about the shape and scale of the sampling distribution is available in an independent manner, and in the similar line we assume that the parameters of to be gamma priors.In many situations, the information about the shape and scale of the sampling distribution is available in an independent manner, and in the similar line we assume that the parameters of 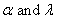 are independent a priori. are independent a priori.
Hence the joint density function is given by
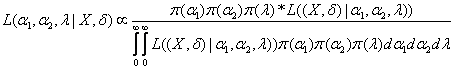
Therefore the Bayes estimator of any function of 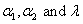 , say g( , say g(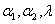 ) is given by ) is given by
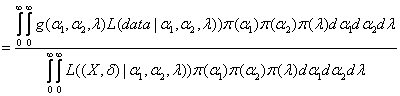
Since it is not possible to compute the function analytically, we use the Markov Chain Monte Carlo (MCMC) method to approximate this function.
|