| |
Example of GED with Complete data
Suppose we have a two component system connected in series. The failure distribution for component 1 and component 2 are given by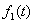 and and 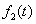 respectively. We assume that the scale parameter ( respectively. We assume that the scale parameter (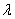 ) for both the components as same and the shape parameters are ) for both the components as same and the shape parameters are 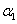 for component 1 and for component 1 and 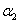 for component 2 respectively. Consider we have n such systems which are identical to each other. We assume that for component 2 respectively. Consider we have n such systems which are identical to each other. We assume that 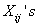 are independent random variables for i=1, 2,…,n and j=1,2 and they are distributed according to Generalized Exponential distribution with parameters ( are independent random variables for i=1, 2,…,n and j=1,2 and they are distributed according to Generalized Exponential distribution with parameters (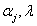 ). ). 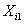 and and 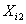 are the time to failure for the ith system due to component 1 and component 2 respectively and are the time to failure for the ith system due to component 1 and component 2 respectively and 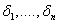 denote the cause of failure for the ith system where denote the cause of failure for the ith system where 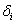 =1, 2. Then, the time to failure for the ith system will be the minimum of the two, i.e., =1, 2. Then, the time to failure for the ith system will be the minimum of the two, i.e., 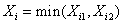 . Then the expected lifetime of the system due to cause 1 is . Then the expected lifetime of the system due to cause 1 is 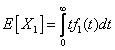 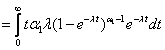 , where , where 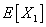 is evaluated using the method of moments and is given by is evaluated using the method of moments and is given by 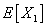 = = 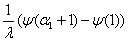 , where , where 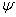 is the digamma function. The relative risk rate ( is the digamma function. The relative risk rate (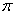 ) due to cause 1 is ) due to cause 1 is 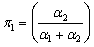 an similarly an similarly 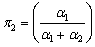 .Suppose that out of the n systems .Suppose that out of the n systems 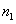 fail due to cause 1 and fail due to cause 1 and 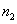 fail due to cause 2. Then the likelihood function for the observed data fail due to cause 2. Then the likelihood function for the observed data 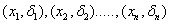 is given by is given by
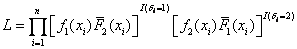
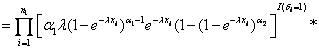
and the log Likelihood Function (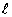 ) is given by ) is given by
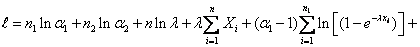
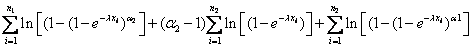 |
(12.8) |
The corresponding likelihood equations can be obtained by taking the partial derivatives with respect to the parameters 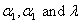 and remembering the fact that for evaluating the MLEs of and remembering the fact that for evaluating the MLEs of 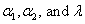 we have to simultaneously solve the set of equations (12.7) and (12.8). As they do not have a closed form solution, hence we use the multidimensional Newton Raphson Method to numerically solve the Likelihood equations to get the MLE estimates we have to simultaneously solve the set of equations (12.7) and (12.8). As they do not have a closed form solution, hence we use the multidimensional Newton Raphson Method to numerically solve the Likelihood equations to get the MLE estimates 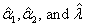 . . |