| |
Case 1: (Generalized Exponential Distribution (GED)) non-Bayesian case
Generalized Exponential (GE) distribution is a three parameter distribution in general. Out of the three parameters, the two parameters for GE distribution are the same as in Gamma and Weibull distribution and they are the scale (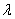 ) and the shape ( ) and the shape (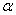 ) parameters. Gamma distribution has been extensively used for analyzing the lifetime data both for its increasing as well as decreasing failure rates which depends upon the shape parameter ( ) parameters. Gamma distribution has been extensively used for analyzing the lifetime data both for its increasing as well as decreasing failure rates which depends upon the shape parameter (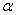 ), but the non existence of any closed form expression for its distribution function resulted in Weibull distribution being used more frequently, since the latter has a closed form expression for its corresponding distribution function. Furthermore GE distribution was given as an option for the Gamma and Weibull distributions and the interesting fact is that this distribution function has closed form expression. GE distribution has likelihood ratio ordering with respect to the shape parameter when the scale parameter is constant, this property is same as that for the Gamma distribution. ), but the non existence of any closed form expression for its distribution function resulted in Weibull distribution being used more frequently, since the latter has a closed form expression for its corresponding distribution function. Furthermore GE distribution was given as an option for the Gamma and Weibull distributions and the interesting fact is that this distribution function has closed form expression. GE distribution has likelihood ratio ordering with respect to the shape parameter when the scale parameter is constant, this property is same as that for the Gamma distribution.
The the three parameter GE along with its survival and hazard function formulae are given as follows
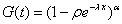 for for 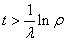 , where , where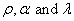 are the respective parameters for the distribution. When are the respective parameters for the distribution. When 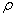 = 1 it is defined as Generalized Exponential (GE) distribution which has the following distribution function = 1 it is defined as Generalized Exponential (GE) distribution which has the following distribution function 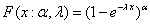 ; ; 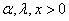 - The density function is
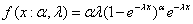 , where , where 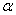 is the shape parameter, is the shape parameter, 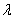 is the scale parameter and finally is the scale parameter and finally 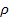 is the location parameter. is the location parameter.
- The corresponding survival function for the GE distribution is given by
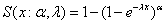
- The hazard function is given as
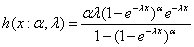
|