| |
If Sc(t), Fc(t), and hc(t), are the hazard rate function or failure rate function, then 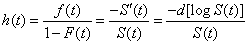 denote the reliability, cumulative distribution function and failure rate for the component, respectively. On the other hand Si(t), Fi(t) and hi(t) are the reliability, distribution function and failure rate for the ith failure mode, respectively. Thus the competing risk model formulas for the component is given by denote the reliability, cumulative distribution function and failure rate for the component, respectively. On the other hand Si(t), Fi(t) and hi(t) are the reliability, distribution function and failure rate for the ith failure mode, respectively. Thus the competing risk model formulas for the component is given by 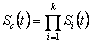 , , 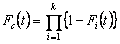 and and 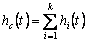 . Now suppose . Now suppose 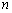 identical units are subject to failure by any one of the identical units are subject to failure by any one of the 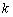 competing risks, then the likelihood function for the observations ( competing risks, then the likelihood function for the observations (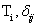 ) where ) where 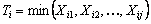 and and 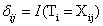 , i =1, 2,….., n is given by , i =1, 2,….., n is given by 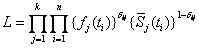 . .
Note : We would like to draw the attendtion of the readers on the first and second part of the likelihood function. Each of them signify two different things. For e.g., let the distribution be exponential, then 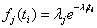 and and 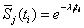 , then the likelihood function is, , then the likelihood function is, 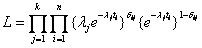 . Now consider there are several mechanisms due to which a system can fail. Since the mechanisms are assumed to be independent to each other, one cannot know beforehand that the system will fail because of which cause, until the system has really failed and the component which fails first causes the system to fail. Under these conditions the component reliability is the product of the failure mode reliabilities and the component failure rate is the sum of failure mode rates. This holds true for any model as long as the condition of 'independence' and the concept of first mechanism failure causes the system to fail is true. . Now consider there are several mechanisms due to which a system can fail. Since the mechanisms are assumed to be independent to each other, one cannot know beforehand that the system will fail because of which cause, until the system has really failed and the component which fails first causes the system to fail. Under these conditions the component reliability is the product of the failure mode reliabilities and the component failure rate is the sum of failure mode rates. This holds true for any model as long as the condition of 'independence' and the concept of first mechanism failure causes the system to fail is true.
Here for our discussion we analyze both (i) Generalized Exponential distribution (GED) and and Lognormal distribution (LN) cases.
Let the number of causes be J (for our study 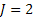 ). Let ). Let 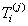 denote the lifetime of ith subject due to cause j (j = 1, 2), where i = 1, 2…..,n. It is assumed that denote the lifetime of ith subject due to cause j (j = 1, 2), where i = 1, 2…..,n. It is assumed that 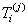 are independent for all i and j, and they are identically distributed for all are independent for all i and j, and they are identically distributed for all 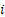 given a value of given a value of 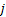 . The corresponding distribution function, density function, survival function and hazard function are given as . The corresponding distribution function, density function, survival function and hazard function are given as 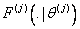 , , 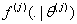 , , 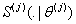 and and 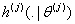 respectively, where respectively, where 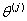 are the real valued parameters for each j. The observed lifetime of ith subject is given by are the real valued parameters for each j. The observed lifetime of ith subject is given by 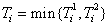 , i.e., the system will fail due to the cause which happens earlier or which occurs first. Our task is to estimate the parameters for these causes assuming they follow a particular density function and find the confidence intervals for these parameter estimates. In a real time situation we can then analyze these causes and their behaviour and try to improve the system. , i.e., the system will fail due to the cause which happens earlier or which occurs first. Our task is to estimate the parameters for these causes assuming they follow a particular density function and find the confidence intervals for these parameter estimates. In a real time situation we can then analyze these causes and their behaviour and try to improve the system.
|