Actual examples of Markov Chains
Let us give a brief set of applications for Markov chains and the areas are:
Internet applications : Markov models can be used to generally understand the browsing characteristics of surfers, such that the web page which appears, depending on the browsing characteristics can be modeled as the state space of the browsing characteristics. Hence if we have 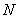 number of web pages which can be visited by a surfer, and each internet page has number of web pages which can be visited by a surfer, and each internet page has 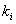 number of links, then the transition probability can be given by the formulae number of links, then the transition probability can be given by the formulae 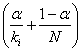 for all the pages that are linked to and for all the pages that are linked to and 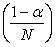 for pages which are not linked to, where for pages which are not linked to, where 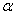 is the transition probability parameter, e.g., the parameter is the transition probability parameter, e.g., the parameter 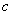 for our earlier example. for our earlier example.
Physics : A sample set of application of Markov process in physics are thermodynamics and statistical mechanics. In general for these physical processes we try to represent the probability for the unknown and hence for specific detail about the equational form of the details of the physical system under study. For example in thermodynamics if we assume the variable, 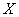 , to be dependent on time then we may model it as a simple stochastic process where the outcome is dictated by both its state and space, such that we can denote it as , to be dependent on time then we may model it as a simple stochastic process where the outcome is dictated by both its state and space, such that we can denote it as 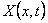 . Similarly in statistical mechanics we have the rate of change of the process given as . Similarly in statistical mechanics we have the rate of change of the process given as 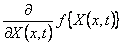 , where one may attempt to find the overall or average property of movement of the particles or in whole of the whole body using stochastic differential equations. , where one may attempt to find the overall or average property of movement of the particles or in whole of the whole body using stochastic differential equations.
Queueing theory : Markov chains is also used for modeling various processes in queueing theory and statistics. In mathematical theory of communication (consider a single step process) in which the stage to which the information/communication moves can be considered as the states and the corresponding probability of the information/communication being transmitted without any los of information is given by the transition probability matrix. What we can do is to find the average rate of information flow and the correlation that message/information/communication once passed/started continues without any loss to a certain probability or certainty.
Chemistry : In crystal or carbon molecular growth (considering we are interested in finding some new combination or a new drug) such that the addition or subtraction of one known molecule of carbon or any other molecule can be consider the state and the probability that the molecule is added or subtracted is considered using it transition probability matrix values.
Statistics : A very interesting application is the use of Markov chain Monte Carlo (MCMC) process. In recent years this has revolutionized the practicability of Bayesian inference methods, allowing a wide range of posterior distributions to be simulated and their parameters found numerically. |