| |
Assignment 1.10
Consider the problem (you have already solved a part of it) as given, in which there are three (3) outcomes, such that the outcomes of any trails are dependent on the outcomes of the previous trial, and the transition probability matrix is given as 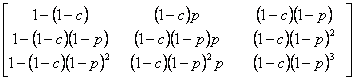 . There are three (3) states given by 0, 1, 2, such that . There are three (3) states given by 0, 1, 2, such that 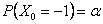 , , 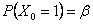 and and 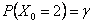 , and , and 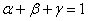 . With this information find (i) . With this information find (i) 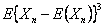 , (ii) , (ii) 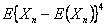 , (iii) , (iii) 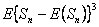 and (iv) and (iv) 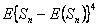 , where , where 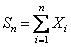 . .
Assignment 1.11
Consider the problem (you have already solved a part of it) as given, in which there are three (3) outcomes, such that the outcomes of any trails are dependent on the outcomes of the previous trial, and the transition probability matrix is given as 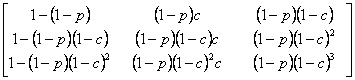 . Assume that we know that there are three (3) states given by -1, 0, +1, such that . Assume that we know that there are three (3) states given by -1, 0, +1, such that 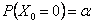 , ,  and and 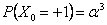 , such that , such that 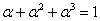 . With this information find (i) . With this information find (i) 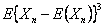 , (ii) , (ii) 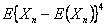 , (iii) , (iii) 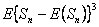 and (iv) and (iv) 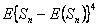 , where , where 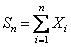 . .
Assignment 1.12
Assume we have a sequence of random walks such that the transition probability matrix is give as 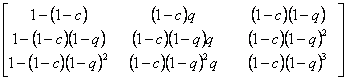 , such that the outcomes of any trails are dependent on the outcomes of the previous trial and , such that the outcomes of any trails are dependent on the outcomes of the previous trial and 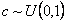 , , 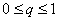 . Also consider that . Also consider that 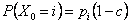 , such that sum of the probability (at the initial stage, t=0) is exactly equal to 1, i.e,, , such that sum of the probability (at the initial stage, t=0) is exactly equal to 1, i.e,, 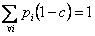 (sum of row elements is exactly equal to 1), and it is also always true that the sum of the realized values of the states at any t=n is exactly equal to six (6), i.e., (sum of row elements is exactly equal to 1), and it is also always true that the sum of the realized values of the states at any t=n is exactly equal to six (6), i.e., 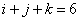 , where , where 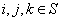 . Given this set of information, find the general formulae for (i) . Given this set of information, find the general formulae for (i) 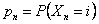 , such that , such that 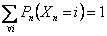 , (ii) , (ii) 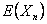 , (iii) , (iii) 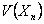 , (iv) , (iv) 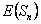 & & 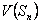 , where , where 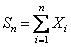 . . |