Economics and finance : In finance and economics Markov chains are used to model a variety of different phenomena, including asset prices and market crashes. Hamilton was the first person to use this methodology successfully in finance where he found the conditional probability of regime switching models or change points such that depending on the states of the process and the corresponding transition probability values one can find the probability that the asset/option prices can be forecasted/predicted with a high degree of accuracy.
Mathematical biology : Applications in biological modeling utilize Markov modeling where a particularly population and its off springs can be models as Markov chain states and the probability that the off springs survives is given by the corresponding transition probability matrix.
Gambling : Markov chains can be used to model many games of chance such as the well know game of snakes and ladders
Concept of Eigen vector and Eigen value
Suppose 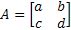 , then , then 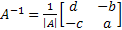 . In that case the Eigen vectors (characteristics equation) is given by . In that case the Eigen vectors (characteristics equation) is given by 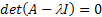
If 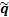 is an eigen vector then we have the following set of equations given by: is an eigen vector then we have the following set of equations given by:
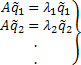 , which means that , which means that 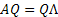 , where , where 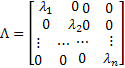 . .
Now as 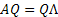 , this implies that , this implies that 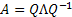 , i.e., , i.e., 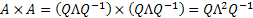 . Moreover . Moreover 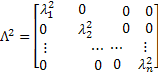 , hence using simple calculation we can immediately find out that , hence using simple calculation we can immediately find out that 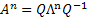 . Thus if . Thus if 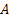 is the transition matrix then is the transition matrix then 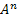 is the n-step transition matrix. is the n-step transition matrix.
|