| |
One may note that 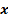 , , 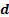 , , 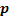 may be continuous, discrete, integer, binary, etc., depending on the scope of the model. Stochasticity in (12.2) comes from two set of variables which are may be continuous, discrete, integer, binary, etc., depending on the scope of the model. Stochasticity in (12.2) comes from two set of variables which are 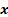 and and 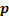 , and for a better illustration of the same one should refer to Figure 12.5 which shows a hypothetical problem with two stochastic inequality constraints (i.e., function of x1 and x2), where, typically the deterministic optimal solution lies on a constraint boundary or at the intersection of more than one constraint, as shown by the red dot (Figure 12.5). , and for a better illustration of the same one should refer to Figure 12.5 which shows a hypothetical problem with two stochastic inequality constraints (i.e., function of x1 and x2), where, typically the deterministic optimal solution lies on a constraint boundary or at the intersection of more than one constraint, as shown by the red dot (Figure 12.5).
In the event of uncertainties in the design/decision variables (i.e., x1 and x2 in this example), there may be instances when the deterministic solution become infeasible, and to find a reliable solution (meaning that there is a very small probability of instances producing an infeasible solution), the true optimal solution is sacrificed and a solution (blue dot, Figure 12.5) in the interior of the feasible region is chosen, such that the level of confidence inside the region marked with blue outline is actually at the specified reliability level, say 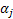 . Thus, for a reliability measure . Thus, for a reliability measure  , it is desired to find the feasible solution that will ensure that the probability of having an infeasible solution is at most , it is desired to find the feasible solution that will ensure that the probability of having an infeasible solution is at most 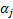 . To incorporate this uncertainty and find the reliable solution, the following probabilistic modification of (12.2), is considered, where in the reliability concept is formulated as the probability of the constraint satisfaction, . To incorporate this uncertainty and find the reliable solution, the following probabilistic modification of (12.2), is considered, where in the reliability concept is formulated as the probability of the constraint satisfaction, 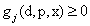 greater than or equal to the desired probability αj. So the probabilistic counter part of (12.2) is shown in (12.3). greater than or equal to the desired probability αj. So the probabilistic counter part of (12.2) is shown in (12.3).
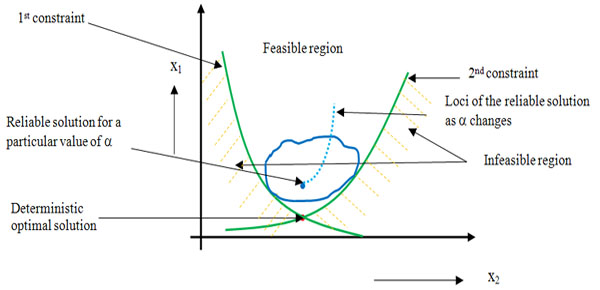
Figure 12.5: Illustration of the concept of Reliability Based Design Optimization (RBDO)

|
(12.3) |
|