| |
An example in optimization and use of reliability based optimization
In optimization problems one tries to find the best possible allocation of resources amongst the probable set of alternatives (feasible sets), to find a unique combination of the control/decision variables, subject to some restrictions/constraints on the control/decision variables domain space, in order to optimize the given objective function(s). Mathematically a generic optimization problem can be stated as given in (12.2).
where (i) 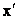 is the objective function which may be linear/non-linear, single/multi-objective, (ii) is the objective function which may be linear/non-linear, single/multi-objective, (ii) 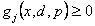 , , 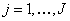 , are the inequality constraints, (iii) , are the inequality constraints, (iii) 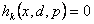 , , 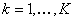 , are the equality constraints, (iv) , are the equality constraints, (iv) 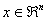 , , 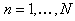 , is the vector of probabilistic control/decision variables, (v) , is the vector of probabilistic control/decision variables, (v) 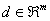 , , 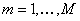 , is the vector of deterministic control/decision variables, and (vi) , is the vector of deterministic control/decision variables, and (vi)  , , 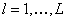 , is the vector of probabilistic exogenous parameters to the system. , is the vector of probabilistic exogenous parameters to the system. |