Concept of Markov Chain Monte Carlo (MCMC) method
A class of algorithms which are used for sampling from a particular population distribution whether of parameter form or non-parametric form such that one can understand the population characteristics using the concept of Markov chain is caled Markov chain Monte Carlo (MCMC) methods. One must remember that MCMC methods include random walk Monte Carlo methods also. For this we use the state of the Markov chain as a sample from the desired distribution, and to achieve this one has to use a large number of steps/iterations to obtain a level of stability. So the quality of the sample improves as a function of the number of steps. Thus in many of the MCMC methods it is advisable that the first 1000 to 5000 iterative run values are disregarded till consistency is achieved. Hence the number of such iterative runs which are to be disregarded depends on the type of Markov chain one has, based on which the sampling plan is being built.
Generally it is easy to know the properties of the Markov Chain, based on which the MCMC works. As already mentioned the difficult part is to determine how many steps are needed to converge to the stationary distribution within an acceptable level of error. A clever way is to start the MCMC method, (based on some Markov chain concept) is to consider an arbitrary initial starting point at each run of the MCMC method, and then allow the MCMC method to continue for 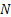 number of times. Repeat the MCMC method with the same Markov chain, but now considering a different starting point, i.e., state. Repeat this large number of times such that the general properties of the MCMC methods are obtained in the long run. The importance of this can be judged from the fact that the states can have different probability, and in the long run it dictates the efficacy of starting at a partcilar state, i. Thus one should continue sampling from the stochastic random process such that one is able to ensure that number of times. Repeat the MCMC method with the same Markov chain, but now considering a different starting point, i.e., state. Repeat this large number of times such that the general properties of the MCMC methods are obtained in the long run. The importance of this can be judged from the fact that the states can have different probability, and in the long run it dictates the efficacy of starting at a partcilar state, i. Thus one should continue sampling from the stochastic random process such that one is able to ensure that 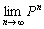 is obtained. It is important to remember that we need to mix the chain in some manner so that stability is achieved such that the values obtained are taken from the actual theoretical distribution, which is very important to us. For the convenience of the reader a simple pseudo-code for the Markov chain Monte Carlo (MCMC) is illustrsted in Figure 12.4. is obtained. It is important to remember that we need to mix the chain in some manner so that stability is achieved such that the values obtained are taken from the actual theoretical distribution, which is very important to us. For the convenience of the reader a simple pseudo-code for the Markov chain Monte Carlo (MCMC) is illustrsted in Figure 12.4.
Pseudo code for MCMC Method

Figure 12.4: Pseudo-code for Markov chain Monte Carlo (MCMC)
Typical use of MCMC sampling can only approximate the target distribution, as there is always some residual effect of the starting point/state. More sophisticated MCMC-based algorithms such as coupling from the past can produce exact samples, at the cost of additional computation and an unbounded (though finite in expectation) running time.
We know that random walk methods are a kind of random simulation or Monte Carlo method. An important thing to note is the fact that the random samples generated during a conventional Monte Carlo integration are statistically independent, but those used in MCMC are correlated. |