Now let us extend these concepts just discussed for the case when we have the figure given as
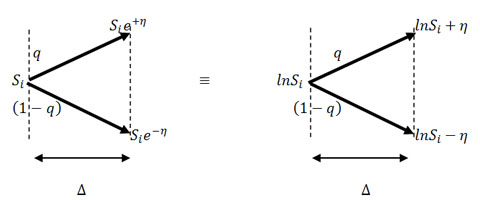
Figure 10.11: A stock and its increase and decrease of price
For the Figure we select 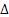 and and 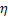 to be small, such that to be small, such that 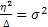 (a constant), and this (a constant), and this 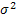 is variance per unit time. Hence it turns out that this random walk converges to a Brownian motion as is variance per unit time. Hence it turns out that this random walk converges to a Brownian motion as 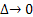 . .
Thus: 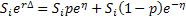 where where 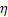 and and 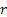 have their usual meaning. have their usual meaning.
Using Taylor series expansion we get 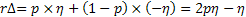 . .
Which results in
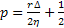
Now when time is taken as 1 we have the following 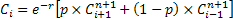 , as true. In the general case when the time period is , as true. In the general case when the time period is 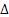 , the equation takes the following form which is , the equation takes the following form which is
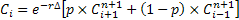 . .
|