Using first order expansion we have
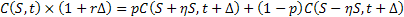
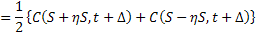
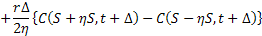
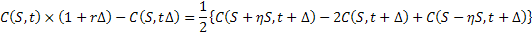
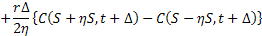
Let us now first divide both sides of the equations with 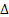 and take limits as and take limits as 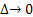 . Furthermore we also divide and simultaneously multiply the first term and the second term on the right hand side of equality by . Furthermore we also divide and simultaneously multiply the first term and the second term on the right hand side of equality by 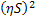 and and 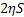 respectively. This results in the following form which is as follows respectively. This results in the following form which is as follows
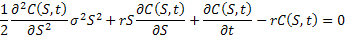
This is the fundamental partial differential equation (PDE) for pricing derivatives under the underlying assumption that logarithmic price of the underlying financial asset has Brownian motion.
In case one is interested to understand how the theoretical relationship between and varies then Figure gives a fair idea how that behaves.
Figure 10.12: Illustration for PDE for pricing derivatives
Recall from Markov Chain Theory that 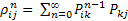 . Now consider a simple random walk with equal probability of a step up and step down i.e., . Now consider a simple random walk with equal probability of a step up and step down i.e., 
|