Thus we have the following
Now if we have only 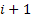 and and 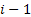 movement then the equation reduces to movement then the equation reduces to
Thus we should have an unique value of 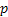 , say , say 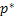 such that the following holds true: such that the following holds true: 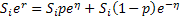 . In fact it can be easily proved for the case when we have only two sates, i.e., . In fact it can be easily proved for the case when we have only two sates, i.e., 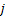 and and 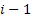 , then , then 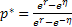 . .
Furthermore combining we can easily see that
Thus we have
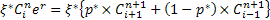 and as and as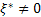 one easily obtains one easily obtains
In general 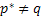 and it reflects the risk premium example. In case and it reflects the risk premium example. In case 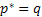 , then we operate in the risk free environment and in that case , then we operate in the risk free environment and in that case 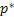 is termed as the risk-neutral probability measure. In general using this value of is termed as the risk-neutral probability measure. In general using this value of 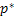 (whether risk free or not is immaterial) we can obtain the discounted expected value of the future claim. (whether risk free or not is immaterial) we can obtain the discounted expected value of the future claim.
|