Example 7.5
Consider a white goods shop, which sells varieties of different capacities of refrigerators, 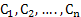 . .
On an average the Ms.Naina Sabarwal, the owner of the shop, has the data that for the best selling
brand/capacity, 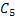 , the average number sold is 3 per day and also that the actual demand follows a , the average number sold is 3 per day and also that the actual demand follows a
Poisson distribution, so she always stocks up 18 number of that product, i.e., 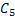 . When the stock . When the stock
level for that particular product, 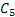 , reaches a value below or equal to 5, a new order of 18 , reaches a value below or equal to 5, a new order of 18
numbers are placed at the beginning of the following week.
With this set of information find the following
(i) The probability of placing an order in any one day of the week
(ii) The average number of that particular product which will be left unsold at the end of the week.
Solution 7.5
(i) The probability of placing an order is given by
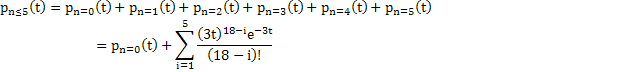
, here 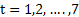 as there are 7 days in a week as there are 7 days in a week
(ii) The average number of product 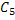 , which will be left unsold at the end of the week , which will be left unsold at the end of the week 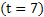 is actually E[n|t=7]. In order to calculate that we need is actually E[n|t=7]. In order to calculate that we need 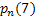 , , 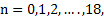 hence the value is hence the value is 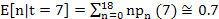 , i.e., about 1. , i.e., about 1.
Consider the following set of information
We have a steady state system where
(i) n: Number of customers/jobs/items in the queue
(ii) 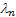 : Arrival rate provided there are n customers/jobs/items in the queue : Arrival rate provided there are n customers/jobs/items in the queue
(iii)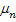 : Departure rate provided there are n customers/jobs/items in the queue : Departure rate provided there are n customers/jobs/items in the queue
(iv) ) 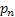 : Steady state probability that there are n customers/jobs/items in the queue : Steady state probability that there are n customers/jobs/items in the queue
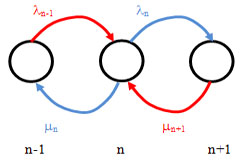
Now for the equilibrium position we must always have I/P is equal to O/P, i.e.,
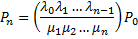
Now remember the diagram for 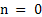 is as given below is as given below
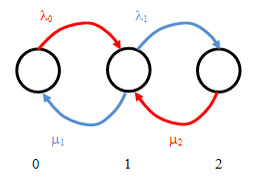
Hence the balance equation is: 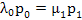 , i.e., , i.e., 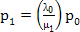
For n = 1, the balance equation is: 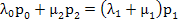 , hence in general we have , hence in general we have
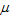 and we know that and we know that 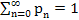
|