Example 7.6
A super market say BigBazar has three check our counters and the store manager knows the following from past data
# of customers |
# of counters |
1 to 3 |
1 |
4 to 6 |
2 |
> 6 |
3 |
If the manager also knows that the mean value of arrival of customers in the store is 10 per hour and the average processing time for the customer is 12 minutes, then find 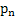 . Why do you think as the store manager this value of . Why do you think as the store manager this value of 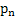 is important for you. is important for you.
Solution 7.6
Now we already have the following set of information. Also remember that the outflow rate is 60/12 =5 customers from the system and the outflow doubles or increases by three the moment you have 2 counters or 3 counters respectively.
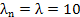
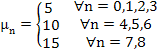
Now utilizing 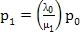 , , 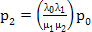 ,…, ,…, 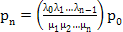 we have we have
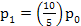 , , 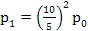 , , 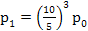
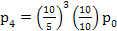 , , 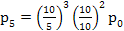 , , 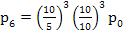
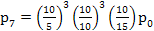 , , 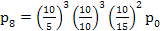 ,….., ,….., 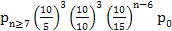
Also 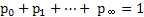 , i.e., , i.e., 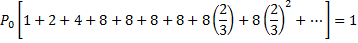
, i.e., using GP series summation we have 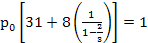 , thus , thus 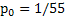
1. So n = 0,1,2,3 we find 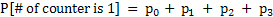
Thus 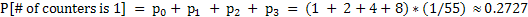
2. So for n = 4,5,6 we find 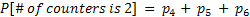
3. So for n = 7,8,… we find 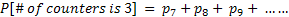
How about finding the expected number of idle counters
If all 3 counters are idle which means the corresponding probability is p0
If 2 counters are idle which means the corresponding probability is 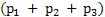
If 1 counter is idle which means the corresponding probability is 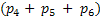
If 0 counters are idle which means the corresponding probability is 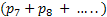
Hence expected value is
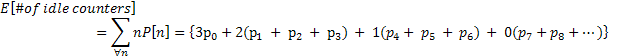
Similarly we can find the E[# of working counters], which would be given by
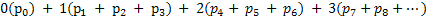
|