Example 7.4
Finished goods come out of the production process on an average every 12 minutes, then find the average production in a week, considering 24 hours utilization every day and 7 days a week.
Solution 7.4
Pure birth process
In general a pure birth process occurs in which ONLY arrivals are allowed. Remember that the exponential distribution will be used to describe the inter-arrival time in a pure birth process.
In a pure birth process we start with 0 number of customers at 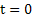 and no queue is considered in the system and we consider arrivals happen at a particular rate which is and no queue is considered in the system and we consider arrivals happen at a particular rate which is 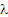 . .
So let us define the following
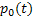 : Probability of no arrivals during a time period of t : Probability of no arrivals during a time period of t
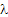 : Average arrival rate of number of customer per unit time : Average arrival rate of number of customer per unit time
Then we have:
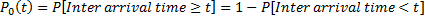
Now for a sufficient small interval time, h > 0, we would have
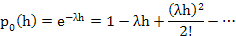 ,further more we can prove that the following also holds and is true which is ,further more we can prove that the following also holds and is true which is 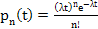 , which is Poisson and the expected value is , which is Poisson and the expected value is 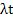 . .
Pure death process
In general a pure death process occurs in which ONLY departures are allowed. Remember that the exponential distribution will be used to describe the inter departure time in a pure death process.
In a pure death process we start with N number of customers at 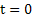 and no new arrivals are considered in the system and we consider departure occurs at a particular rate which is and no new arrivals are considered in the system and we consider departure occurs at a particular rate which is 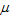 . .
So let us define the following
p0(t): Probability of no departures during a time period of t
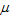 : Average departure rate of number of customer per unit time : Average departure rate of number of customer per unit time
Using similarly we can prove that
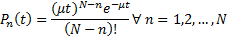
where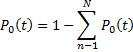 .Now remember that the following equations we have, is the truncated Possion distribution. .Now remember that the following equations we have, is the truncated Possion distribution.
|