| |
Such that 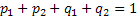 , and , and 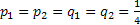
Consider a battery operated car which can move randomly along the tracks in right, left, up, down with some fixed probability, where these probabilities do not change. Also consider the floor or plane to be infinite, i.e., there are infinite number of such states, or places the car can move. If 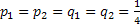 , we will see whether the origin from where the car starts is recurrent or not. Now if the car moves , we will see whether the origin from where the car starts is recurrent or not. Now if the car moves 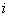 units to right, units to right, 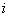 units to left, units to left, 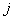 units to up and finally units to up and finally 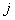 units to down, such that, , units to down, such that, , 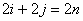 then we have the following then we have the following
(i) 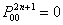 , 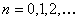 and
(ii) 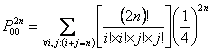 , , 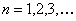
Here we apply multinomial distribution to find the second term given above. |