| |
Note:
Can you guess what happens in general when we have 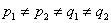 , and the movements are , and the movements are 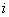 units to right, units to right, 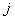 units to left, units to left, 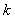 units to up and units to up and 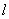 units to down, such that, units to down, such that, 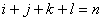 . Comment intelligently on this problem. . Comment intelligently on this problem.
Again let us continue with the problem which we were discussing. So we have
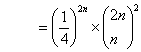 as 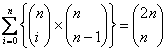 |
Using Stirling's formula or approximation, which is 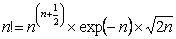 , we have , we have 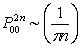 . Again let us pay attention to the fact that . Again let us pay attention to the fact that 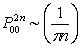 when when 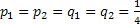 , hence the rate of convergence for , hence the rate of convergence for 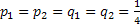 is not zero, else the rate of convergence of is not zero, else the rate of convergence of 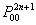 is 0. So now we have the sequence is 0. So now we have the sequence 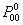 , , 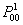 , …., and the sum, i.e., , …., and the sum, i.e., 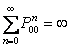 iff iff 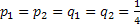 . Thus the two dimension random walk is recurrent iff . Thus the two dimension random walk is recurrent iff 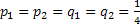 . .
|