Let us pay attention to the fact that 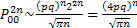 and this lead us to the fact that and this lead us to the fact that 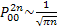 for the case when for the case when 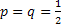 , else the rate of convergence of , else the rate of convergence of 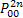 is is 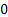 . So now we have the sequence . So now we have the sequence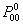 , , 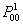 , …., and the sum, i.e., , …., and the sum, i.e., 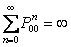 iff iff 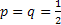 . Thus the one dimension random walk is recurrent iff . Thus the one dimension random walk is recurrent iff 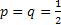 , else it is transient, i.e., we have convergence. , else it is transient, i.e., we have convergence.
Example 1.19
Can you say something of two dimensional random walk of the form, which is illustrated below, in the case when we have
(i) Probability of moving up is 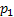
(ii) Probability of moving down 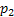
(iii)Probability of moving right 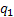
(iv)Probability of moving left 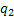
|